S8.


Solution:

It is known, the relation between the transfer characteristic and the weighting function is:
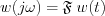
$ w(j \omega)=\mathfrak{F} \left { w(t) \right }

It is possible to see from the given figures
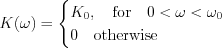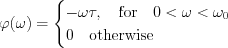
$ K(\omega) = \begin{cases} K_0,\quad \text{for}\quad 0<\omega < \omega_0 \\ 0 \quad \text{otherwise} \end{cases} and $ \varphi(\omega)= \begin{cases} -\omega \tau,\quad \text{for} \quad 0<\omega < \omega_0 \\ 0 \quad \text{otherwise} \end{cases}

Consequently, the formula of the transfer characteristic is the following:
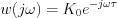$ w(j\omega)=K_0e^{-j\omega \tau} , for $ 0<\omega < \omega_0, otherwise $ 0 .

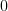The weighting function can be derived by the inverse Fourier transformation of the transfer characteristic:

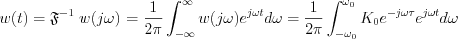
$ w(t)=\mathfrak{F}^{-1} \left { w(j\omega) \right }= \frac{1}{2\pi} \int_{-\infty}^{\infty}w(j\omega)e^{j\omega t} d\omega = \frac{1}{2\pi} \int_{-\omega_0}^{\omega_0}K_0 e^{-j\omega \tau}e^{j\omega t} d\omega

$ w(t)= \frac{1}{2\pi} \int_{-\omega_0}^{\omega_0}K_0 e^{j\omega( t-\tau )} d\omega = \frac{1}{2\pi} K_0 \left [ \frac{e^{j\omega( t-\tau )}}{j(t-\tau)} \right ] _{-\omega_0}^{\omega_0}=\frac{ K_0 }{2\pi} \left [\frac{e^{j\omega_0( t-\tau )}}{j(t-\tau)}- \frac{e^{-j\omega_0( t-\tau )}}{j(t-\tau)} \right ]

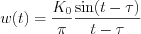
$ w(t)= \frac{ K_0 }{\pi}\frac{\text{sin}(t-\tau)}{t-\tau}

 
(Return to the Problems)


The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=S8.