S5.


Solution:

Let’s apply another way to solve the differential equation, i.e. do the Laplace transformation of both side of the equation!

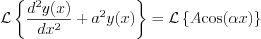
$ \mathcal{L}\left\{\frac{d^{2}y(x)}{dx^{2}}+a^{2}y(x)\right\} = \mathcal{L}\left\{A\text{cos}(\alpha x)\right\}

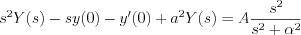
$ s^{2}Y(s)-sy(0)-y'(0)+a^{2}Y(s) = A\frac{s^{2}}{s^{2}+\alpha^{2}}

Let’s substitute the initial conditions, i.e. 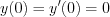$y(0)=y'(0)=0

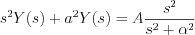
$ s^{2}Y(s)+a^{2}Y(s) = A \frac{s^{2}}{s^{2}+\alpha^{2}}

$ Y(s)\left[s^{2}+a^{2}\right]=A\frac{s^{2}}{s^{2}+\alpha^{2}}

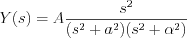
$ Y(s)=A\frac{s^{2}}{(s^{2}+a^{2})(s^{2}+\alpha^{2})}

$y(x) function can be determined by the inverse Laplace transformation!

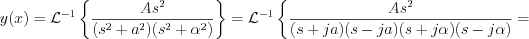
$ y(x)=\mathcal{L}^{-1}\left\{\frac{As^{2}}{(s^{2}+a^{2})(s^{2}+\alpha^{2})}\right\}=\mathcal{L}^{-1}\left\{\frac{As^{2}}{(s+ja)(s-ja)(s+j\alpha)(s-j\alpha)}=
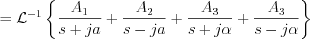$ =\mathcal{L}^{-1}\left\{\frac{A_{1}}{s+ja}+\frac{A_{2}}{s-ja}+\frac{A_{3}}{s+j\alpha}+\frac{A_{3}}{s-j\alpha}\right\} , where the method of partial fraction is working, and very useful, but in the particular case would be very long calculation with many traps. Let’s try another way now, i.e. let’s apply some algebraic conversions.

$Y(s) = A\frac{s^{2}}{(s^{2}+a^{2})(s^{2}+\alpha^{2})}=A\frac{s^{2}(s^{2}+a^{2})-s^{4}-s^{2}(s^{2}+\alpha^{2})+s^{4}}{(s^{2}+a^{2})(s^{2}+\alpha^{2})}\frac{1}{a^{2}-\alpha^{2}}=\frac{A}{a^{2}-\alpha^{2}}\left[\frac{s^{2}}{s^{2}+\alpha^{2}}-\frac{s^{2}}{s^{2}+a^{2}}\right]

Let’s execute the inverse Laplace transformation now!

$ y(x)=\mathcal{L}^{-1}\left\{Y(s)\right\} = \mathcal{L}^{-1}\left\{\frac{A}{a^{2}-\alpha^{2}}\left[\frac{s^{2}}{s^{2}+\alpha^{2}}-\frac{s^{2}}{s^{2}+a^{2}}\right] \right\} = \frac{A}{a^{2}-\alpha^{2}}\left[\mathcal{L}\left\{\frac{s^{2}}{s^{2}+\alpha^{2}}-\frac{s^{2}}{s^{2}+a^{2}}\right\} \right]

$ y(x)=\frac{A}{a^{2}-\alpha^{2}}\left[\text{cos}(\alpha x)-\text{cos}(ax)\right]

 
(Return to the Problems)


The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=S5.