S4.


Solution:

Let’s try to find the complementary function of the second ordered linear differential equation with constant coefficients at first.

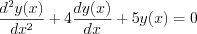
$ \frac{d^{2}y(x)}{dx^{2}}+4\frac{dy(x)}{dx}+5y(x) = 0

Let’s find the complementary function by the following formula 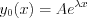$y_{0}(x)=Ae^{\lambda x}

 
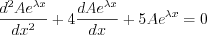
$ \frac{d^{2}Ae^{\lambda x}}{dx^{2}}+4\frac{dAe^{\lambda x}}{dx}+5Ae^{\lambda x} = 0

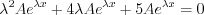
$ \lambda^{2}Ae^{\lambda x}+4\lambda Ae^{\lambda x} + 5Ae^{\lambda x} = 0

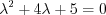$ \lambda^{2}+4\lambda+5=0 where the auxiliary equation is obtained. Roots of the second ordered polynomial equation:

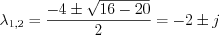
$ \lambda_{1,2}=\frac{-4 \pm \sqrt{16-20}}{2}=-2 \pm j
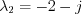i.e. $\lambda_{1}=-2+j and $\lambda_{2}=-2-j.

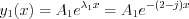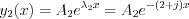
Consequently the solutions are $ y_{1}(x)=A_{1}e^{\lambda_{1}x}=A_{1}e^{-(2-j)x} and $ y_{2}(x)=A_{2}e^{\lambda_{2}x}=A_{2}e^{-(2+j)x}

Linear combination of the two independent solution is also solution of the homogenous equation, meaning the complementary function will be the following:
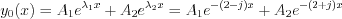
$ y_{0}(x)=A_{1}e^{\lambda_{1}x}+A_{2}e^{\lambda_{2}x}=A_{1}e^{-(2-j)x}+A_{2}e^{-(2+j)x}

Let’s find the particular solution as 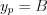$y_{p}=B, where B is a constant value, due to the constant input function.

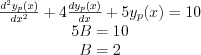
$ \begin{matrix} \frac{d^{2}y_{p}(x)}{dx^{2}}+4\frac{dy_{p}(x)}{dx}+5y_{p}(x)=10\\ 5B = 10\\ B=2 \end{matrix}

General solution of the inhomogeneous differential equation is:

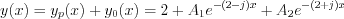
$ y(x)=y_{p}(x)+y_{0}(x)=2+A_{1}e^{-(2-j)x}+A_{2}e^{-(2+j)x}

Let’s use the initial conditions, in order to determine 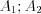$A_{1};A_{2} coefficients.

$ \left.\begin{matrix} y(0)=0\\ \\ \frac{dy(x)}{dx}\big{|}_{x=0}=0 \end{matrix}\right\}\rightarrow\begin{matrix} 2+A_{1}+A_{2}=0 \\ \\ \frac{dy(x)}{dx}\big{|}_{x=0}=\frac{d}{dx}\left[2+A_{1}e^{-(2-j)x}+A_{2}e^{-(2+j)x}\right]\big{|}_{x=0}=-(2-j)A_{1}-(2+j)A_{2}=0 \end{matrix}

Now the following set of two linear equations has to solve:
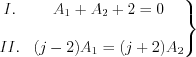
$\left.\begin{matrix} I. & A_{1}+A_{2}+2=0\\ \\ II.& (j-2)A_{1}=(j+2)A_{2} \end{matrix}\right\}

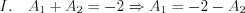
$ I.\quad A_{1}+A_{2} = -2 \Rightarrow A_{1} = -2-A_{2}

Let’s substitute the A1 coefficient into the II. equation

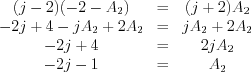$ \begin{matrix} (j-2)(-2-A_{2})&=&(j+2)A_{2}\\ -2j+4-jA_{2}+2A_{2}&=&jA_{2}+2A_{2}\\ -2j+4&=&2jA_{2}\\ -2j-1&=&A_{2} \end{matrix},
as well as 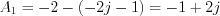$A_{1}=-2-(-2j-1)=-1+2j.

Consequently the general solution of the differential equation is:

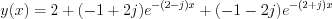
$ y(x)=2+(-1+2j)e^{-(2-j)x}+(-1-2j)e^{-(2+j)x}

$ y(x)=2+(-1+2j)e^{-2x}e^{jx}+(-1-2j)e^{-2x}e^{-jx}=2+e^{-2x}\left[(-1+2j)e^{jx}-(1+2j)e^{-jx}\right]

$ y(x)=2+e^{-2x}\left[-e^{jx}+2je^{jx}-e^{-jx}-2je^{-jx}\right]

$ y(x)=2+e^{-2x}\left[-(e^{jx}+e^{-jx})+2j(e^{jx}-e^{-jx})\right]

The following expression can be written by Euler’s formula:
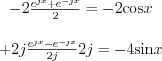
$ \begin{matrix} -2\frac{e^{jx}+e^{-jx}}{2}=-2\text{cos}x\\ \\ +2j\frac{e^{jx}-e^{-jx}}{2j}2j=-4\text{sin}x \end{matrix}

The solution is $y(x)=2+e^{-2x}\left[-2\text{cos}x-4\text{sin}x\right]

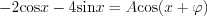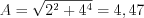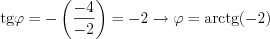
Let’s do some conversion at the final formula: it is known, that $ -2\text{cos}x-4\text{sin}x=A\text{cos}(x+\varphi), where $A=\sqrt{2^{2}+4^{4}}=4,47, and $\text{tg}\varphi=-\left(\frac{-4}{-2}\right)=-2 \rightarrow \varphi = \text{arctg}(-2)

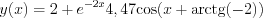
$y(x)=2+e^{-2x}4,47\text{cos}(x+\text{arctg}(-2))

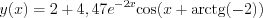
$y(x)=2+4,47e^{-2x}\text{cos}(x+\text{arctg}(-2))

 
(Return to the Problems)


The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=S4.