Parzeval-tétel

Az alábbiakban azt mutatjuk meg, hogy maga az 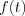$f(t) függvény, illetve annak energia tartalma miként határozható meg a komplex spektrum reális illetve imaginárius részek ismeretében.
A komplex spektrum a Fourier transzformációval nyerhető:

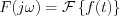
$$ F(j\omega) = \mathcal{F}\left\{f(t)\right\}$

ahol $$ \left.\begin{matrix} 2Re\left[F(j\omega) \right ]= A(\omega)\\ -2Im\left[F(j\omega)\right]=B(\omega) \end{matrix}\right\}$

Ezen jelölések bevezetésével 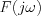$$F(j\omega)$ eképp írható fel:

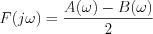
$$ F(j\omega) = \frac{A(\omega)-B(\omega)}{2}$

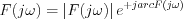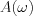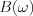Következésképpen az $$ F(j\omega) = \left|F(j\omega)\right|e^{+jarcF(j\omega)}$ az $$A(\omega)$ és $$B(\omega)$ paraméterekkel az alábbiak szerint fejezhető ki:

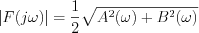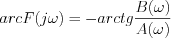
$$ \left | F(j\omega) \right | = \frac{1}{2}\sqrt{A^{2}(\omega)+B^{2}(\omega)}$ és $$ arcF(j\omega)=-arctg\frac{B(\omega)}{A(\omega)}$

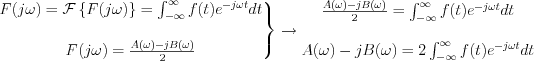
$$ \left.\begin{matrix} F(j\omega)=\mathcal{F} \left \{F(j\omega){ \right \} = \int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\\ \\ F(j\omega)=\frac{A(\omega)-jB(\omega)}{2} \end{matrix}\right\} \rightarrow \begin{matrix} \frac{A(\omega)-jB(\omega)}{2} = \int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\\ \\ A(\omega)-jB(\omega) = 2 \int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt \end{matrix}$

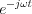Az $$e^{-j\omega t}$ -re vonatkozóan alkalmazzuk az Euler relációt: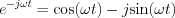 $$e^{-j\omega t} = \text{cos}(\omega t)-j\text{sin}(\omega t)$

$$A(\omega)-jB(\omega) = 2 \left[\int_{-\infty}^{\infty}f(t)e^{-j\omega t}dt\right] = 2\left[\int_{-\infty}^{\infty}f(t)\text{cos}(\omega t)dt-j\int_{-\infty}^{\infty}f(t)\text{sin}(\omega t)dt\right]$

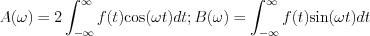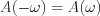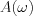$$A(\omega) = 2\int_{-\infty}^{\infty}f(t)\text{cos}(\omega t)dt; B(\omega) = \int_{-\infty}^{\infty}f(t)\text{sin}(\omega t)dt$ . Ezen összefüggésekből leolvasható, hogy $$A(-\omega) = A(\omega)$ azaz $$A(\omega)$ páros, míg 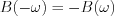$$B(-\omega) = -B(\omega)$ páratlan függvények.

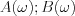$$A(\omega);B(\omega)$ és az inverz Fourier transzfomáció formulája alapján f(t) eképp írható fel:

$$f(t) = \mathcal{F}^{-1}\left\{F(j\omega)\right\} = \frac{1}{2\pi} \int_{-\infty}^{\infty}\frac{A(\omega)-jB(\omega)}{2}e^{j\omega t}d\omega = \frac{1}{4\pi}\int_{-\infty}^{\infty}\left[A(\omega)-jB(\omega)\right]\left[\text{cos}(\omega t)+j\text{sin}(\omega t)\right]d\omega$

$$f(t) = \frac{1}{4\pi} \int_{-\infty}^{\infty}\left[A(\omega)\text{cos}(\omega t)+B(\omega)\text{sin}(\omega t)\right]d\omega + \frac{1}{4\pi}j\int_{-\infty}^{\infty}\left[A(\omega)\text{sin}(\omega t)-B(\omega)\text{cos}(\omega t)d\omega$

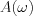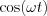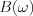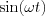Mivel $$A(\omega)$ is és $$\text{cos}(\omega t)$ páros illetve $$B(\omega)$ és $$\text{sin}(\omega t)$ páratlan, ezért szorzatuk eredménye mindkét esetre vonatkozóan páros lesz. Ennek következménye, hogy az impropirus integrál ezen része páros függvényen történik. Teljesen analóg módon belátható, hogy az impropirus integrál másik tagja páratlan függvényen történik, és így ezen rész impropirus integrélja 0.

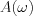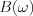Így $$f(t) = \frac{1}{4\pi} \int_{-\infty}^{\infty}\left[A\text{cos}(\omega t) + B\text{sin}(\omega t)\right]d\omega = \frac{1}{2\pi}\int_{0}^{\infty}\left[A(\omega)\text{cos}(\omega t)+B(\omega)\text{sin}(\omega t)\right]d\omega$ kifejezhető az $$A(\omega)$ és $$B(\omega)$ ismeretében.

Az 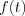$f(t) függvény energiatartalma:

$$ E=\frac{1}{2\pi}\int_{-\infty}^{\infty}\left|F(j\omega)\right|^{2}d\omega = \frac{1}{2\pi}\int_{-\infty}^{\infty}\frac{1}{4}\left[A^{2}(\omega) + B^{2}(\omega)\right]d\omega = \frac{1}{\pi}\int_{0}^{\infty}\frac{1}{4}\left[A^{2}(\omega)+B^{2}(\omega)\right]d\omega =$

$$= \frac{1}{4\pi}\int_{0}^{\infty} \left[A^{2}(\omega)+B^{2}(\omega)\right]d\omega$

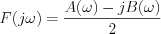hiszen $$F(j\omega) = \frac{A(\omega)-jB(\omega)}{2}$ és $$ \left|F(j\omega)\right|^{2} = \frac{1}{4}\left[A^{2}(\omega) + B^{2}(\omega)\right]$

(Vissza a 'Fourier-transzformáció' című fejezethez)

The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=Parzeval-t%C3%A9tel