Interpretation of the inverse Radon transform

Analysis of the Fourier inversion formula

$$ \frac{1}{2}\left (\frac{1}{2\pi} \right )^{n-1}\int_{\mathbb{S}^{n-1}}\int_{-\infty}^{\infty} \mathfrak{F}\left [ f \right ]\left ( r\boldsymbol{\omega} \right)\left | r \right |^{n-1} e^{ir\mathbf{x} \boldsymbol{\omega }}dr d\boldsymbol{\omega }= \frac{1}{2}\left (\frac{1}{2\pi} \right )^{n-1}\int_{\mathbb{S}^{n-1}} \mathfrak{F}^{-1}_{r} \left [ \mathfrak{F}_{t}\mathfrak{R}f \right ] \left | r \right |^{n-1} d\boldsymbol{\omega }$
Let us look at the terms of the inversion formula again.

The adjoint to the Radon-transform

For the outermost integral 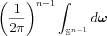$$ \left (\frac{1}{2\pi} \right )^{n-1}\int_{\mathbb{S}^{n-1}} d\boldsymbol{\omega }$ we have already introduced the notation of 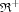$$\mathfrak{R^{+}}$ . To an 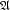$$\mathfrak{A}$ operator the definition of the adjoint 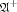$$\mathfrak{A^{+}}$ operator reads:
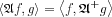
$$ \left \langle \mathfrak{A}f,g \right \rangle=\left \langle f,\boldsymbol{\mathfrak{A}^{+}}g \right \rangle$
here <f,g> is the scalar product of f and g . The adjoint to the Radon transform is the backprojection operator:
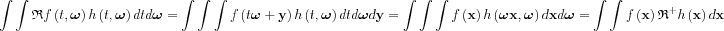
$$ \int \int \mathfrak{R}f\left ( t,\boldsymbol{\omega }\right )h\left ( t,\boldsymbol{\omega } \right )dtd\boldsymbol{\omega }=\int\int \int f\left ( t\boldsymbol{\omega }+\mathbf{y}\right )h\left (t, \boldsymbol{\omega } \right )dtd\boldsymbol{\omega }d\mathbf{y}=\int\int \int f\left ( \mathbf{x}\right )h\left (\boldsymbol{\omega }\mathbf{x}, \boldsymbol{\omega } \right )d\mathbf{x}d\boldsymbol{\omega }=\int \int f\left ( \mathbf{x}\right )\mathfrak{R}^{+}h\left (\mathbf{x} \right )d\mathbf{x}$
Here we have changed variables from the original t and y to the rotated x variables in the integration.

The Hilbert transform hidden in the Radon inversion formula

In the next step let us look at the terms disregarding the backprojection operator:
$$ \mathfrak{F}^{-1}_{r} \left [ \mathfrak{F}_{t}\mathfrak{R}f \right ] \left | r \right |^{n-1}=\mathfrak{F}^{-1}_{r}\left ( -ir \right)^{n-1}\left ( i sgn(r)\right)^{n-1} \left [ \mathfrak{F}_{t}\mathfrak{R}f \right ]$
In general it is true to a funcion g that
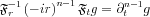
$$\mathfrak{F}^{-1}_{r} \left ( -ir \right )^{n-1} \mathfrak{F}_{t} g= \partial _{t}^{n-1}g$
We have shown about the Hilbert Transform that
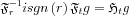
$$ \mathfrak{F}^{-1}_{r} i sgn\left ( r \right ) \mathfrak{F}_{t} g= \mathfrak{H}_{t} g$
from this:
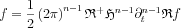
$$ f=\frac{1}{2}\left ( 2\pi \right )^{n-1}\mathfrak{R}^{+}\mathfrak{H}^{n-1}\partial_{t}^{n-1}\mathfrak{R}f$
As the sgn function is present, the formula
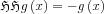$$\mathfrak{H}\mathfrak{H}g\left ( x \right )=-g\left ( x \right )$ behaves differently depending on whether n is even or odd.

Now we can also write the odd and even terms separately:
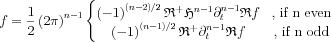
$$ f=\frac{1}{2}\left ( 2\pi \right )^{n-1}\left\{\begin{matrix} \left (-1 \right )^{\left (n-2 \right )/2}\mathfrak{R}^{+}\mathfrak{H}^{n-1}\partial_{t}^{n-1}\mathfrak{R}f & \text{, if n even}\\ \left (-1 \right )^{\left (n-1 \right )/2}\mathfrak{R}^{+}\partial_{t}^{n-1}\mathfrak{R}f & \text{, if n odd} \end{matrix}\right.$

The lack of the Hilbert transform in the even dimensions have a fundamental impact:

when the Hilbert transform is missing from the formula, for the reconstruction of a certain point of the distribution we need the Radon transform on hyperplanes going through only the small neighborhood of the point
when the Hilbert transform is present, for the reconstruction at a point we need the whole sinogram

Note that at n=2 we obtain Radon's inversion formula. There are further analytical solutions to the inverse Radon problem, we will be dealing with that in the next section.

The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=Interpretation+of+the+inverse+Radon+transform