Filter Design for the Filtered Backprojection

The formula for filtered backprojection can be generalized in a more practical way than was shown with the Riesz potentials, now we will look at the convolution form. Let 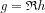$$ g=\mathfrak{R}h$ the Radontransform in n dimensions. Let us prove that
$$ \mathfrak{R}^{+}g*_{\mathbf{x}}f=\mathfrak{R}^{+}\left [ g*_{t}\mathfrak{R}f \right ]$
where the indices to the convolution sign * indicate the variables of the convolution.
The LHS convolution with the our usual notations:
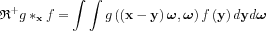
$$\mathfrak{R}^{+}g*_{\mathbf{x}}f=\int\int g\left ( \mathbf{\left (x-y \right )\boldsymbol{\omega }}, \boldsymbol{\omega }\right )f\left ( \mathbf{y} \right )d\mathbf{y}d\boldsymbol{\omega }$
Let us replace variable y with 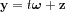$$ \mathbf{y}=t\boldsymbol{\omega }+\mathbf{z}$ , here z is perpendicular to $$\boldsymbol{\omega }$ -ra. Then inserting:
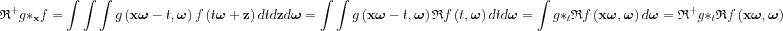
$$ \mathfrak{R}^{+}g*_{\mathbf{x}}f=\int \int\int g\left ( \mathbf{x\boldsymbol{\omega }}-t, \boldsymbol{\omega }\right )f\left ( t\boldsymbol{\omega }+\mathbf{z} \right )dtd\mathbf{z}d\boldsymbol{\omega }= \int\int g\left ( \mathbf{x}\boldsymbol{\omega }-t, \boldsymbol{\omega }\right )\mathfrak{R}f\left ( t,\boldsymbol{\omega } \right )dtd\boldsymbol{\omega }= \int g*_{t}\mathfrak{R}f\left ( \mathbf{x}\boldsymbol{\omega },\boldsymbol{\omega } \right )d\boldsymbol{\omega }=\mathfrak{R}^{+} g*_{t}\mathfrak{R}f\left ( \mathbf{x}\boldsymbol{\omega },\boldsymbol{\omega } \right )$

Let us now choose the following V and v functions:
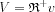
$$ V= \mathfrak{R}^{+}v$
Inserting:
$$V*_{\mathbf{x}}f=\mathfrak{R}^{+}\left [ v*_{t}\mathfrak{R}f \right ]$

Let us look for such V functions that in a given band limit approximate the Dirac delta function so the original f function would be restored. It can be proven that
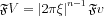
$$\mathfrak{F}V=\left |2\pi \xi \right |^{n-1}\mathfrak{F}v$
thus, if the Fourier transform of Vis a constant within the bandlimits, for v a family of filters can be designed. If we only allow for radial dependence of the filters we get our previous filtered backprojection formulas.

The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=Filter+Design+for+the+Filtered+Backprojection