Deriving of Fourier Theory, Fourier Series

In this chapter it will bel shown, how it is possible to derive the periodic functions as a function series. First, let′s take into account the analysis of continuous functions. Next, consider the following defined and continuously differentiable function set in [a;b] interval.
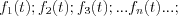
f_1(t); f_2(t); f_3(t); ... f_n(t)...;

Furthermore, let′s consider the defined and infinitely continuously differentiable f(t) function in [a;b] interval. The question is the following. Is it possible to express f(t) as infinite function series:
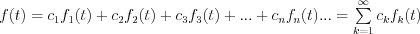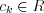
$f(t) = c_1 f_1(t)+c_2 f_2(t)+c_3 f_3(t) +...+c_n f_n(t)... = \sum\limits_{k = 1}^\infty c_k f_k(t)$ where $c_k \in R$

It is well known, that a defined and infinitely continuously differentiable f(t) function in [a;b] interval can be expressed as power series as follow:
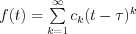
$f(t) = \sum\limits_{k = 1}^\infty c_k(t-\tau)^k$
where in current case
$f(t)_k=(t-\tau)^k$ , and c_k is the Taylor coefficient
$c_k = \frac{\frac{df}{dt}}{k!} \Big|_{t=\tau} = \frac{f^{(k)}(t) }{k!}$
Consequently $f(t) = \sum\limits_{k=1}^\infty \frac{f^{(k)} (t)}{k!} c_k(t-\tau)^k$

Next let′s consider, when 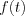f(t) is a periodic function i.e. 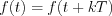f(t)=f(t+kT) in [a;b] interval, where T ͼ R is the period of f(t) and k=1,2, .....n,.. natural numbers.
Let′s attempt to derive the 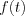f(t) periodic function in [a;b] interval as the superposition of trigonometric functions as follow:
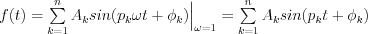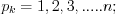$f(t) = \sum\limits_{k=1}^n A_k sin(p_k\omega t +\phi_k) \Big|_{\omega = 1} = \sum\limits_{k=1}^n A_k sin(p_k t +\phi_k)$ where p_k=1,2,3, .....n; natural numbers and let′s suppose 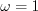$\omega = 1$ as the fundamental period of trigonometric function.

Then apply the trigonometric addition sum theorem for the trigonometric function series:
$f(t) = \sum\limits_{k=1}^n A_k sin(p_k t +\phi_k) = \sum\limits_{k=1}^n A_k [sin(p_k t)cos(\phi_k) + cos(p_k t)sin(\phi_k)] = = \sum\limits_{k=1}^n [ (A_k cos(\phi_k)) sin(p_k t)+(A_k sin(\phi_k)) cos(p_k t) ]$
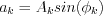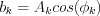
Let's use the following denote: $a_k = A_k sin(\phi_k)$ , $b_k = A_k cos(\phi_k)$
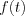Thus $f(t) = \sum\limits_{k=1}^n [a_k sin(p_k t) + b_k cos(p_kt)]$ , which means the f(t) periodic function may be approximated by a finite trigonometric series.

Consequently, the following problems have to be faced:

Is it possible to find any series for f(t), i.e. if f(t) is a periodic function is it possible to express it as a superposition of trigonometric functions?
Can f(t) function be expressed as a finite or infinite trigonometric series?
If f(t) can be expressed as finite or infinite series, then how is possible to determine the 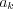, and 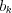coefficients?

Since f(t) periodic function is attempted to be expressed as the superposition of trigonometric functions, see the following denotes with the corresponding series elements:
Let 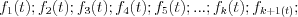$f_1(t); f_2(t); f_3(t); f_4(t); f_5(t); ...; f_k(t); f_{k+1(t)};$ functions
and 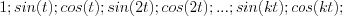1; sin(t); cos(t); sin(2t); cos(2t); ...; sin(kt); cos(kt); trigonometric function be elements of the series.

The mathematical question: is it possible to describe f(t) periodic function by infinite trigonometric series as follow: $f(t)= A_0 + \sum\limits_{k=1}^\infty [a_k cos(kt) + b_k sin(kt)]$

Since the series is based on trigonometric function elements, let′s suppose the period of f(t) is 2π, i.e. f(t)=f(t+2kπ) (period of the elements of the trigonometric series are 2π too). Furthermore, let′s suppose the trigonometric series representing the f(t) periodic function is consistently convergent in [-∞;∞].
Then multiply both side of the following expression by cos(nt) and sin(nt) as shown below:
f $f(t)= A_0 + \sum\limits_{k=1}^\infty [a_k cos(kt) + b_k sin(kt)]$

The following two expressions are obtained after the multiplications:
$f(t)cos(nt)= A_0 cos(nt) + \sum\limits_{k=1}^\infty [a_k cos(kt)cos(nt) + b_k sin(kt)cos(nt)]$
$f(t)sin(nt)= A_0 sin(nt) + \sum\limits_{k=1}^\infty [a_k cos(kt)sin(nt) + b_k sin(kt)sin(nt)]$

Since the trigonometric series is consistently convergent and |cos(nt)|≤ 1 as well as |sin(nt)|≤ 1, thus the multiplication by cos(nt) and sin(nt) will keep the consistently convergence. Due to the consistently convergence the elements of trigonometric series can be integrated by members in [a; a+2π] interval:
$\int\limits_a^{a+2\pi} f(t)cos(nt)= A_0 \int\limits_a^{a+2\pi} cos(nt) + \sum\limits_{k=1}^\infty \int\limits_a^{a+2\pi} [a_k cos(kt)cos(nt) + b_k sin(kt)cos(nt)]$
$\int\limits_a^{a+2\pi} f(t)sin(nt)= A_0 \int\limits_a^{a+2\pi} sin(nt) + \sum\limits_{k=1}^\infty \int\limits_a^{a+2\pi} [a_k cos(kt)sin(nt) + b_k sin(kt)sin(nt)]$ ,
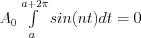where $A_0 \int\limits_a^{a+2\pi} sin(nt)dt=0$ , as well as 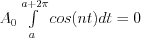$A_0 \int\limits_a^{a+2\pi} cos(nt)dt=0$ due to the result of one period definite integral of the trigonometric function.
Consequently, the two integral can be described as follow:
$\int\limits_a^{a+2\pi} f(t)cos(nt)dt= \sum\limits_{k=1}^\infty { \int\limits_a^{a+2\pi}[a_k cos(kt)cos(nt) + b_k sin(kt)cos(nt)]dt}$
$\int\limits_a^{a+2\pi} f(t)sin(nt)dt= \sum\limits_{k=1}^\infty { \int\limits_a^{a+2\pi}[a_k cos(kt)sin(nt) + b_k sin(kt)sin(nt)]dt}$
The next step is to analyze the integrals behind the ∑ expressions. Trigonometric addition sum theorem is applied in the analysis:
$\int\limits_a^{a+2\pi} a_k cos(kt)sin(nt)dt = (a_k/2) \int\limits_a^{a+2\pi} [sin(n-k)t + sin(n+k)t]dt = (a_k/2) \int\limits_a^{a+2\pi} sin(n-k)tdt + (a_k/2) \int\limits_a^{a+2\pi} sin(n+k)tdt=0$
Within the definite integral operation you can find sin(mt) and sin(qt) type of expressions, where m=n-k and q=n+k and they have 2π period too. Consequently, these definite integrals are zero (see above).

Following a similar procedure result in: 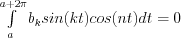$\int\limits_a^{a+2\pi} b_k sin(kt)cos(nt)dt=0$

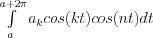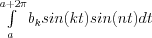
The next step is to determine the following definite integrals: $\int\limits_a^{a+2\pi} a_k cos(kt)cos(nt)dt$ and $\int\limits_a^{a+2\pi} b_k sin(kt)sin(nt)dt$

Two cases are considered. First, when n≠k:
$\int\limits_a^{a+2\pi} a_k cos(kt)cos(nt)dt = (a_k/2) \int\limits_a^{a+2\pi}[cos(k+n)t + cos(k-n)t]dt = =(a_k/2) \int\limits_a^{a+2\pi} cos(k+n)tdt + (a_k/2) \int\limits_a^{a+2\pi} cos(k-n)tdt = 0$
$\int\limits_a^{a+2\pi} b_k sin(kt)sin(nt)dt = (b_k/2) \int\limits_a^{a+2\pi} [cos(k+n)t - cos(k-n)t]dt = = (b_k/2) \int\limits_a^{a+2\pi} cos(k+n)tdt - (b_k/2) \int\limits_a^{a+2\pi} cos(k-n)tdt = 0$
because of considerations already made above.

Next case is, when n=k:
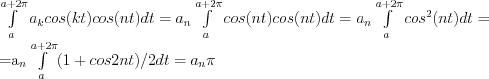
$\int\limits_a^{a+2\pi} a_k cos(kt)cos(nt)dt = a_n \int\limits_a^{a+2\pi} cos(nt)cos(nt)dt = a_n \int\limits_a^{a+2\pi} cos^2(nt)dt = =a_n \int\limits_a^{a+2\pi} (1+cos2nt)/2 dt = a_n \pi$
and 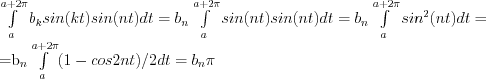$\int\limits_a^{a+2\pi} b_k sin(kt)sin(nt)dt = b_n \int\limits_a^{a+2\pi} sin(nt)sin(nt)dt = b_n \int\limits_a^{a+2\pi} sin^2(nt)dt = =b_n \int\limits_a^{a+2\pi} (1-cos2nt)/2 dt = b_n \pi$

Thus the results of the definite integrals:
$\int\limits_a^{a+2\pi} f(t)cos(nt)dt=\sum\limits_{k=1}^\infty { \int\limits_a^{a+2\pi} [a_k cos(kt)cos(nt) + b_k sin(kt)cos(nt)]dt}= a_n \pi \rightarrow a_n = 1/\pi \int\limits_a^{a+2\pi} f(t)cos(nt)dt$
$\int\limits_a^{a+2\pi} f(t)sin(nt)dt= { \int\limits_a^{a+2\pi} [a_k cos(kt)sin(nt) + b_k sin(kt)sin(nt)]dt}= b_n \pi \rightarrow b_n =1/\pi \int\limits_a^{a+2\pi} f(t)sin(nt)dt$

Consequently, if f(t) is periodic f(t)=f(t+2nπ) and consistently convergent , then it can be expressed as a trigonometric series as follow: $f(t)= A_0 + \sum\limits_{k=1}^\infty [a_k cos(kt) + b_k sin(kt)]$ , where the coefficients are:
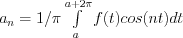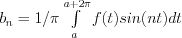
$a_n = 1/\pi \int\limits_a^{a+2\pi} f(t)cos(nt)dt$ , and $b_n =1/\pi \int\limits_a^{a+2\pi} f(t)sin(nt)dt$

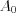The A_0 constant can be derived as follow: $f(t)= A_0 + \sum\limits_{k = 1}^\infty [a_k cos(kt)+b_k sin(kt)]= \sum\limits_{k = 0}^\infty [a_k cos(kt)+b_k sin(kt)]$

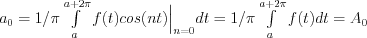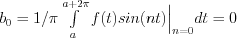
Consequently: $a_0 = 1/\pi \int\limits_a^{a+2\pi} f(t)cos(nt) \Big|_{n=0} dt =1/ \pi \int\limits_a^{a+2\pi} f(t)dt = A_0$ and $b_0 =1/\pi \int\limits_a^{a+2\pi} f(t)sin(nt) \Big|_{n=0} dt = 0$

The original document is available at http://537999.nhjqzg.asia/tiki-index.php?page=Deriving+of+Fourier+Theory%2C+Fourier+Series